Program Optimization Experiments

Program optimization is a very intresting problem. With the different matrix-multiply program, I want to find the factors which might have influence on the performace of the programs. Several experiments has been conducted on my computer. Source code and results will be listed as follow. Also, I will give a brief analysis and some simple conclusions on them. Machine Information can be found here

1 There Loops Resolution

1.1 Source Code

#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include <string.h>
#include <sys/time.h>

#define DIM 4096
typedef double(* MATRIX)[DIM];

void multiply(MATRIX z, const MATRIX x, const MATRIX y, int dim)
{
    int row, col, idx;
    double tmp;
    for (row = 0; row < dim; row++)
        for (col = 0; col < dim; col++) {
            tmp = 0;
            for (idx = 0; idx < dim; idx++)
                tmp += x[row][idx] * y[idx][col];
            z[row][col] = tmp;
        }
}

void init_matrix(MATRIX m, int dim, int isRandom)
{
    int row, col;
    if (isRandom) {
        srandom(time(NULL));
        for (row = 0; row < dim; row++)
            for (col = 0; col < dim; col++)
                m[row][col] = random() % 263;
    } else
        memset((void *)m, 0, dim * dim * sizeof(m[0][0]));
}

void print_matrix(MATRIX m, int dim)
{
    int row, col;
    for (row = 0; row < dim; row++) {
        for (col = 0; col < dim; col++)
            printf("%f ", m[row][col]);
        printf("\n");
    }
}

int main(void)
{
    MATRIX x = (MATRIX)malloc(DIM*DIM*sizeof(double));
    MATRIX y = (MATRIX)malloc(DIM*DIM*sizeof(double));
    MATRIX z = (MATRIX)malloc(DIM*DIM*sizeof(double));
    init_matrix(x, DIM, 1);
    init_matrix(y, DIM, 1);
    init_matrix(z, DIM, 0);
    struct timeval start, end;
    gettimeofday(&start, NULL);
    multiply(z, x, y, DIM);
    gettimeofday(&end, NULL);
    int time = (int)(end.tv_sec-start.tv_sec);
    unsigned long long opts = (unsigned long long)DIM*DIM*(2*DIM-1);
    double speed = opts / (double)(time * 1000000);
    printf("%d matrix multiply\n", DIM);
    printf("time : %ds\tspeed: %.2f MFLOPS\n", time, speed);
    return 0;
}

1.2 Results

1.2.1 No Optimization

ict-lxb@ictlxb-Zhaoyang-E49:~/Workspace/test$ ./matrix
4096 matrix multiply
time : 1038s    speed: 132.39 MFLOPS

1.2.2 -O2 Optimization

ict-lxb@ictlxb-Zhaoyang-E49:~/Workspace/test$ ./matrix_O2 
4096 matrix multiply
time : 944s speed: 145.57 MFLOPS

1.3 Conclusion

After analysing the results above, we can see that the same source code compiled with different optimization options might result in very different performance. The compiler can improve the performance by reordering the instructions, which might cause bubble in the instruction parallel, and so on.

2 Three Loops Resulotion (4097X4097)

2.1 Source Code

#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include <string.h>
#include <sys/time.h>

#define DIM 4097
typedef double(* MATRIX)[DIM];

void multiply(MATRIX z, const MATRIX x, const MATRIX y, int dim)
{
    int row, col, idx;
    double tmp;
    for (row = 0; row < dim; row++)
        for (col = 0; col < dim; col++) {
            tmp = 0;
            for (idx = 0; idx < dim; idx++)
                tmp += x[row][idx] * y[idx][col];
            z[row][col] = tmp;
        }
}

void init_matrix(MATRIX m, int dim, int isRandom)
{
    int row, col;
    if (isRandom) {
        srandom(time(NULL));
        for (row = 0; row < dim; row++)
            for (col = 0; col < dim; col++)
                m[row][col] = random() % 263;
    } else
        memset((void *)m, 0, dim * dim * sizeof(m[0][0]));
}

void print_matrix(MATRIX m, int dim)
{
    int row, col;
    for (row = 0; row < dim; row++) {
        for (col = 0; col < dim; col++)
            printf("%f ", m[row][col]);
        printf("\n");
    }
}

int main(void)
{
    MATRIX x = (MATRIX)malloc(DIM*DIM*sizeof(double));
    MATRIX y = (MATRIX)malloc(DIM*DIM*sizeof(double));
    MATRIX z = (MATRIX)malloc(DIM*DIM*sizeof(double));
    init_matrix(x, DIM, 1);
    init_matrix(y, DIM, 1);
    init_matrix(z, DIM, 0);
    struct timeval start, end;
    gettimeofday(&start, NULL);
    multiply(z, x, y, DIM-1);
    gettimeofday(&end, NULL);
    int time = (int)(end.tv_sec-start.tv_sec);
    //unsigned long long opts = (unsigned long long)DIM*DIM*(2*DIM-1);
    int n = DIM-1;
    unsigned long long opts = (unsigned long long)n*n*(2*n-1);
    double speed = opts / (double)(time * 1000000);
    printf("%d matrix multiply\n", DIM);
    printf("time : %ds\tspeed: %.2f MFLOPS\n", time, speed);
    return 0;
}

2.2 Results

ict-lxb@ictlxb-Zhaoyang-E49:~/Workspace/test$ ./matrix_4097 
4097 matrix multiply
time : 901s speed: 152.52 MFLOPS

2.3 Conclusion

After analysing the results above, we can see that the performance was improved due in large part to cache miss rate decreasing. 4097 matrix might decrease the

collision of cache line becuase of its irregular layout.

3 Three Loops Resulotion With Transpose

3.1 Source Code

#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include <string.h>
#include <sys/time.h>

#define DIM 4096
typedef double(* MATRIX)[DIM];

void transpose(MATRIX m, int dim)
{
    int row, col;
    double tmp;
    for (row = 1; row < dim; row++)
        for (col = 0; col < row; col++) {
            tmp = m[row][col];
            m[row][col] = m[col][row];
            m[col][row] = tmp;
        }
}

void multiply(MATRIX z, const MATRIX x, const MATRIX y, int dim)
{

    int row, col, idx;
    double tmp;
    transpose(y, dim);
    for (row = 0; row < dim; row++)
        for (col = 0; col < dim; col++) {
            tmp = 0;
            for (idx = 0; idx < dim; idx++)
                tmp += x[row][idx] * y[col][idx];
            z[row][col] = tmp;
        }
}

void init_matrix(MATRIX m, int dim, int isRandom)
{
    int row, col;
    if (isRandom) {
        srandom(time(NULL));
        for (row = 0; row < dim; row++)
            for (col = 0; col < dim; col++)
                m[row][col] = random() % 263;
    } else
        memset((void *)m, 0, dim * dim * sizeof(m[0][0]));
}

void print_matrix(MATRIX m, int dim)
{
    int row, col;
    for (row = 0; row < dim; row++) {
        for (col = 0; col < dim; col++)
            printf("%f ", m[row][col]);
        printf("\n");
    }
}

int main(void)
{
    MATRIX x = (MATRIX)malloc(DIM*DIM*sizeof(double));
    MATRIX y = (MATRIX)malloc(DIM*DIM*sizeof(double));
    MATRIX z = (MATRIX)malloc(DIM*DIM*sizeof(double));
    init_matrix(x, DIM, 1);
    init_matrix(y, DIM, 1);
    init_matrix(z, DIM, 0);
    struct timeval start, end;
    gettimeofday(&start, NULL);
    multiply(z, x, y, DIM);
    gettimeofday(&end, NULL);
    int time = (int)(end.tv_sec-start.tv_sec);
    unsigned long long opts = (unsigned long long)DIM*DIM*(2*DIM-1);
    double speed = opts / (double)(time * 1000000);
    printf("%d matrix multiply\n", DIM);
    printf("time : %ds\tspeed: %.2f MFLOPS\n", time, speed);
    return 0;
}

3.2 Results

ct-lxb@ictlxb-Zhaoyang-E49:~/Workspace/test$ ./matrix_transpose 
4096 matrix multiply
time : 72s  speed: 1908.64 MFLOPS

3.3 Conclusion

After analysing the results above, we can see that the performance is improved so much. The reasons for that might be that the array in C program language is row-major and that cache miss rate decreases due to the transpose. Temporal locality and spatial locality is the key point in this improvement.

4 Three Loops Resulotion With Partition

4.1 Source Code

#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include <string.h>
#include <sys/time.h>

#define B 128
#define DIM 4096
typedef double(* MATRIX)[DIM];

#define MIN(x, y) ((x) > (y) ? (y) : (x))

void multiply(MATRIX z, const MATRIX x, const MATRIX y, int dim)
{
    int row, col, idx, ri, ci;
    double tmp;
    for (row = 0; row < dim; row+=B)
        for (col = 0; col < dim; col+=B)
            for (ri = 0; ri < dim; ri++)
                for (ci = col; ci < MIN(dim, col+B); ci++) {
                    tmp = 0;
                    for (idx = col; idx < MIN(dim, col+B); idx++)
                        tmp += x[ri][idx] * y[idx][ci];
                    z[ri][ci] += tmp;
                }
}

void init_matrix(MATRIX m, int dim, int isRandom)
{
    int row, col;
    if (isRandom) {
        for (row = 0; row < dim; row++)
            for (col = 0; col < dim; col++)
                m[row][col] = random() % 263;
    } else
        memset((void *)m, 0, dim * dim * sizeof(m[0][0]));
}

void print_matrix(MATRIX m, int dim)
{
    int row, col;
    for (row = 0; row < dim; row++) {
        for (col = 0; col < dim; col++)
            printf("%f ", m[row][col]);
        printf("\n");
    }
}

int main(void)
{
    srandom(time(NULL));
#if 1
    MATRIX x = (MATRIX)malloc(DIM*DIM*sizeof(double));
    MATRIX y = (MATRIX)malloc(DIM*DIM*sizeof(double));
    MATRIX z = (MATRIX)malloc(DIM*DIM*sizeof(double));
    init_matrix(x, DIM, 1);
    init_matrix(y, DIM, 1);
    init_matrix(z, DIM, 0);
#else
    double x[DIM][DIM] = {
        {1, 2},
        {3, 4}
    };
    double y[DIM][DIM] = {
        {4, 3},
        {2, 1}
    };
    double z[DIM][DIM] = {
        {0, },
    };
#endif
    struct timeval start, end;
    gettimeofday(&start, NULL);
    multiply(z, x, y, DIM);
    gettimeofday(&end, NULL);
    int time = (int)(end.tv_sec-start.tv_sec);
    unsigned long long opts = (unsigned long long)DIM*DIM*(2*DIM-1);
    double speed = opts / (double)(time * 1000000);
    printf("%d matrix multiply\n", DIM);
    printf("time : %ds\tspeed: %.2f MFLOPS\n", time, speed);
#if 0
    print_matrix(x, DIM);
    print_matrix(y, DIM);
    print_matrix(z, DIM);
#endif
    return 0;
}

4.2 Results

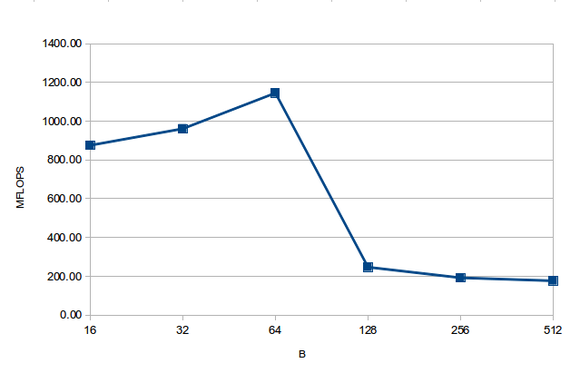
b-mflops

4.3 Conclusion

After analysing the results above, we can see that the performance is optimal when B is 64.

5 Serial Program Analysis

From all the experiments above, we can see that the bottlenect of the serial program (matrix multiply) is memory access delay. With some optimization such as instructions reordering by compilers, improving temporal locality and spatial locality of data, the performance could be improved due to less cache misses.

6 Optimal Program With Pthread

6.1 Source Code

#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include <string.h>
#include <sys/time.h>
#include <pthread.h>

#define CORES 2
#define THREADS 4
#define WORKERS (THREADS)


#define DIM 4096
#define COL (DIM/WORKERS)
typedef double(* MATRIX)[DIM];

typedef struct {
    MATRIX x;
    MATRIX y;
    MATRIX z;
    int row_start;
    pthread_t pid;
} Arguments;

Arguments argument[WORKERS] = { {0, }, };

void print_matrix(MATRIX m, int dim)
{
    int row, col;
    for (row = 0; row < dim; row++) {
        for (col = 0; col < dim; col++)
            printf("%f ", m[row][col]);
        printf("\n");
    }
}

void transpose(MATRIX m, int dim)
{
    int row, col;
    double tmp;
    for (row = 1; row < dim; row++)
        for (col = 0; col < row; col++) {
            tmp = m[row][col];
            m[row][col] = m[col][row];
            m[col][row] = tmp;
        }
}

void multiply(MATRIX z, const MATRIX x, const MATRIX y, int row_offset)
{
    int row, col, idx;
    double tmp;
    int end = row_offset + COL;
    for (row = row_offset; row < end; row++)
        for (col = 0; col < DIM; col++) {
            tmp = 0;
            for (idx = 0; idx < DIM; idx++)
                tmp += x[row][idx] * y[col][idx];
            z[row][col] = tmp;
        }
}

void* worker(void *arg)
{
    Arguments* args = (Arguments* )arg;
    multiply(args->z, args->x, args->y, args->row_start);
}

void init_matrix(MATRIX m, int dim, int isRandom)
{
    int row, col;
    if (isRandom) {
        srandom(time(NULL));
        for (row = 0; row < dim; row++)
            for (col = 0; col < dim; col++)
                m[row][col] = random() % 263;
    } else
        memset((void *)m, 0, dim * dim * sizeof(m[0][0]));
}

int main(void)
{
    int i;
    MATRIX x = (MATRIX)malloc(DIM*DIM*sizeof(double));
    MATRIX y = (MATRIX)malloc(DIM*DIM*sizeof(double));
    MATRIX z = (MATRIX)malloc(DIM*DIM*sizeof(double));
    init_matrix(x, DIM, 1);
    init_matrix(y, DIM, 1);
    init_matrix(z, DIM, 0);
    struct timeval start, end;
    gettimeofday(&start, NULL);
    transpose(y, DIM);
    for (i = 1; i < WORKERS; i++) {
        argument[i].x = x;
        argument[i].y = y;
        argument[i].z = z;
        argument[i].row_start = i * COL;
        pthread_create(&argument[i].pid, NULL, worker, &argument[i]);
    }
    multiply(z, x, y, 0);
    for (i = 1; i < WORKERS; i++)
        pthread_join(argument[i].pid, NULL);
    gettimeofday(&end, NULL);
    int time = (int)(end.tv_sec-start.tv_sec);
    unsigned long long opts = (unsigned long long)DIM*DIM*(2*DIM-1);
    double speed = opts / (double)(time * 1000000);
    printf("%d matrix multiply with %d workers\n", DIM, WORKERS);
    printf("time : %ds\tspeed: %.2f MFLOPS\n", time, speed);
    return 0;
}

6.2 Results

ict-lxb@ictlxb-Zhaoyang-E49:~/Workspace/test$ ./matrix_pthread 
4096 matrix multiply with 2 workers
time : 49s  speed: 2804.53 MFLOPS

ict-lxb@ictlxb-Zhaoyang-E49:~/Workspace/test$ ./matrix_pthread 
4096 matrix multiply with 4 workers
time : 31s  speed: 4432.97 MFLOPS

ict-lxb@ictlxb-Zhaoyang-E49:~/Workspace/test$ ./matrix_pthread 
4096 matrix multiply with 8 workers
time : 44s  speed: 3123.23 MFLOPS

ict-lxb@ictlxb-Zhaoyang-E49:~/Workspace/test$ ./matrix_pthread 
4096 matrix multiply with 16 workers
time : 43s  speed: 3195.86 MFLOPS

...

ict-lxb@ictlxb-Zhaoyang-E49:~/Workspace/test$ ./matrix_pthread 
4096 matrix multiply with 4096 workers
time : 42s  speed: 3271.96 MFLOPS

rate = 72 / 49 = 1.47
rate = 72 / 31 = 2
rate = 72 / 44 = 1.64

6.3 Conclusion

After analysing the results above, we can see that the performance is imporved so much that 4096 matrix multiply with 16 workers took only 43 seconds. Parallel optimization can improve the performance in a reasonable way. However, With the number of workers increasing, the performance did not decrease as expected, I guess thread switch might be optimized so well that the cost could be ignored.

7 Optimization With BLAS (optional)

(To be continued)

blog comments powered by Disqus

Published

03 May 2014

Program Optimization Experiments matrix multiply